Huit solutions

La non-transitivité des amitiés (malgré le dicton bien connu selon lequel les amis de mes amis sont mes amis), évoqué il y a quelques semaines , est clairement liée au paradoxe sorite. Car, aussi minime soit-elle, il existe toujours une « distance » (d'idées, de caractère, de comportement, etc.) entre deux personnes. Ainsi, la somme de proximités peut devenir insurmontable, tout comme un magasin près d'un autre magasin près de chez vous peut se trouver à l'autre bout de la ville si l'on intercale suffisamment de proximités.

Concernant les huit points de la semaine dernière, quelques réponses rapides ou seulement sommaires et d'autres plus détaillées :

1. On nous dit que la femme n'a pas la peau foncée, et la personne aux cheveux blonds répond, donc elle doit avoir les cheveux blancs, ergo…

2. Quant au triangle obtus à diviser en angles aigus, il est facile d'arriver à la fausse conclusion que c'est impossible (Martin Gardner a dit qu'à son époque il avait reçu plusieurs « démonstrations » d'une telle impossibilité), car peu importe combien on le divise, il finit toujours par y avoir au moins un petit angle obtus tenace, comme celui du sommet inférieur droit de la figure.

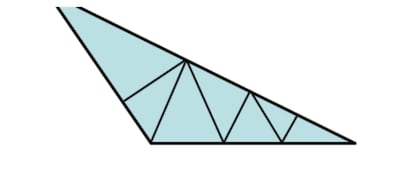
Cependant, la division est possible, et pour vous donner un indice , je dirai que c'est l'un de ces problèmes instructifs où nous nous imposons inconsciemment plus de conditions que ce qu'on nous demande de remplir. Quelle est, dans ce cas, la condition inconsciente et non sollicitée ?

3. Il y avait cinq frères Marx : Chico, Groucho, Harpo, Gummo et Zeppo ; mais pour les besoins de notre énigme, la solution la plus probable est qu'ils étaient quatre (comme dans leurs films les plus célèbres) et que trois d'entre eux étaient gauchers. Cette solution n'est pas unique : il pourrait aussi y avoir 21 frères, dont 15 gauchers. Existe-t-il une autre solution, même si elle est démographiquement peu plausible ?

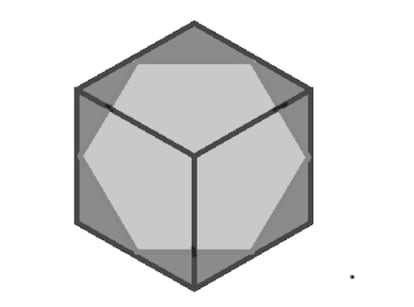
4. Si le plan de coupe passe par les milieux de six arêtes du cube, on obtient un hexagone régulier.

5. 129 + 438 = 567 (Cette solution est-elle unique ?).

6. Si OODDF est la racine carrée de WONDERFUL, O ne peut être supérieur à 2, puisque son carré aurait dix chiffres, et il ne peut être 1, puisque le carré d' un nombre commençant par 11 ne peut avoir un 1 dans son deuxième chiffre ; donc, O = 2. Le nombre cherché sera donc compris entre les carrés de 22 000 et 23 000, et puisque le deuxième chiffre de WONDERFUL est 2, W = 5… En suivant ce raisonnement, on obtient WONDERFUL = 523 814 769.

7. Le plus grand cercle qui ne traverse que des carrés blancs a son centre au centre d'un carré blanc et passe par les sommets les plus éloignés des quatre carrés noirs qui l'entourent. (Quel est son rayon ?)

8. Les trains s'approchent à une vitesse relative de 130 + 170 = 300 km/h, donc 5 minutes avant la collision, ils seront à 25 km l'un de l'autre. La distance initiale est sans importance ; elle ne sert qu'à induire en erreur.

Jeux non transitifs

Concernant la non-transitivité, Salva Fuster a commenté : « Les dés non-transitifs sont l'un des cas les plus surprenants que je connaisse. Je pense que la plupart des gens qui voient des dés non-transitifs pour la première fois essaient de trouver l'erreur en comptant les cas où chaque dé en surpasse un autre. » C'est tout à fait vrai et intéressant, à tel point qu'un prochain article mériterait d'être consacré à ce sujet. Et pour vous mettre en appétit, pensez à un autre jeu non-transitif. Il en existe au moins deux très populaires…