Восемь решений

Нетранзитивность дружеских отношений (вопреки известному высказыванию «друзья моих друзей — мои друзья»), поднятая пару недель назад , явно связана с парадоксом Сорита. Ведь, какой бы малой она ни была, между двумя людьми всегда существует «дистанция» (идей, характера, поведения и т. д.). Следовательно, сумма близости может стать непреодолимой дистанцией, подобно тому, как магазин, находящийся рядом с магазином, который находится рядом с магазином, который находится рядом с магазином, который находится рядом с магазином... который находится рядом с вашим домом, может оказаться на другом конце города, если мы добавим достаточно близости.

Что касается восьми вопросов прошлой недели, некоторые быстрые или лишь отрывочные ответы , а другие более подробные:

1. Нам говорят, что женщина не смуглая, а отвечает человек со светлыми волосами, значит, у нее должны быть белые волосы, следовательно…

2. Что касается деления тупоугольного треугольника на острые углы, то легко прийти к ложному выводу, что это невозможно (Мартин Гарднер говорил, что в свое время он получил несколько «демонстраций» такой невозможности), потому что, сколько бы мы его ни делили, всегда останется по крайней мере один маленький и неподатливый тупой угол, подобный тому, что находится в правой нижней вершине фигуры.

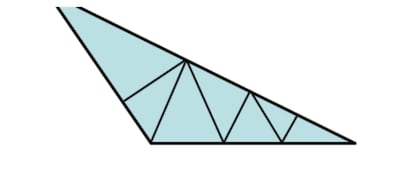
Однако разделение возможно, и в качестве подсказки скажу, что это одна из тех поучительных задач, где мы бессознательно навязываем себе больше условий, чем нам предписано выполнять. Что же в данном случае является бессознательным, непрошеным условием?

3. Братьев Маркс было пятеро: Чико, Граучо, Харпо, Гуммо и Зеппо. Но для нашей загадки наиболее вероятным решением будет то, что их было четверо (как в самых известных фильмах), и трое из них были левшами. Это решение не единственное: братьев может быть 21, 15 из которых — левши. Есть ли другое решение, даже если оно демографически неправдоподобно?

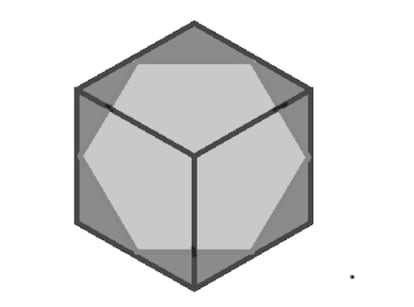
4. Если секущая плоскость пройдет через середины шести рёбер куба, то получим правильный шестиугольник.

5. 129 + 438 = 567 (Является ли это решение единственным?).

6. Если ООДДФ — квадратный корень ЧУДЕСНОГО, то О не может быть больше 2, так как его квадрат будет содержать десять цифр, и не может быть равен 1, так как квадрат числа, начинающегося с 11, не может иметь 1 во второй цифре; следовательно, О = 2. Таким образом, искомое число будет лежать между квадратами 22 000 и 23 000, а поскольку вторая цифра ЧУДЕСНОГО равна 2, то О = 5… Продолжая эту цепочку рассуждений, получаем ЧУДЕСНОЕ = 523 814 769.

7. Самый большой круг, проходящий только через белые квадраты, имеет центр в центре белого квадрата и проходит через самые удалённые вершины четырёх чёрных квадратов, окружающих его. (Каков его радиус?)

8. Поезда сближаются с относительной скоростью 130 + 170 = 300 км/ч, поэтому за 5 минут до столкновения они будут находиться на расстоянии 25 км друг от друга. Начальное расстояние не имеет значения и служит лишь для того, чтобы ввести в заблуждение.

Нетранзитивные игры

Что касается нетранзитивности, Сальва Фустер прокомментировал: «Нетранзитивные игральные кости — один из самых удивительных случаев, известных мне. Думаю, большинство людей, впервые видящих нетранзитивные игральные кости, пытаются найти ошибку, подсчитывая случаи, когда каждая кость побеждает другую». Очень верно и интересно, настолько, что стоит посвятить этой теме отдельный пост. А чтобы подогреть интерес, вспомните ещё одну нетранзитивную игру. Есть как минимум две очень популярные…