Papierosy w kontakcie

Nasz klaustrofobiczny podróżnik z zeszłego tygodnia postąpiłby mądrze, wsiadając do ostatniego wagonu. Na pierwszy rzut oka wydaje się, że każdy samochód jest taki sam; Ale ponieważ tunel znajduje się przy wyjściu ze stacji, pociąg wjeżdżając do niego będzie nadal przyspieszał, więc ostatni wagon przejedzie przez niego szybciej niż pozostałe. Ponadto, jak zauważyli Salva Fuster i Francisco Montesinos, pasażerowie mogą biec do przodu po wejściu do tunelu, więc ich prędkość zostanie dodana do prędkości pociągu, co da względną wyższą prędkość przejazdu.

W przypadku równowagi nierównych ramion jest to podchwytliwe pytanie (nie możemy zapominać, że są to problemy zadawane przez złośliwe dziecko): odpowiedź brzmi tak… pod warunkiem, że jest to średnia geometryczna , a nie średnia arytmetyczna, jak zwykliśmy myśleć, gdy mówimy po prostu „średnia”.

Problem kwadratowych płytek wywołał liczne komentarze i różne sposoby jego rozwiązania. Najprostsze, najbardziej eleganckie i pomysłowe rozwiązanie zaproponował Manuel Amorós. Nazywając a i b liczbą kwadratów na boku każdego kwadratu, a n liczbą elementów, mamy:

n + 7 = a²

n – 10 = b²

z czym odejmując drugą równość od pierwszej:

(a + b)(a – b) = 17

z czego wynika, że ​​a + b = 17, a – b = 1

więc n = 74

Dla tych, którzy uważają, że to zbyt krótkie wyjaśnienie, przypomnijmy sobie zasadę „sumy przez różnicę, różnicy kwadratów” oraz to, że 17, będąc liczbą pierwszą, może zostać rozłożona jedynie na dwa czynniki w postaci 17 = 1 x 17.

Równie zwięzłe i eleganckie rozwiązanie proponuje María Luisa González w wariancie z dominem:

Kwadrat z domina utworzono za pomocą X x 2X kostek domina, zatem:

(X x 2X) – 1 = (X – 1)(2X – 2) + 13

Rozwiązanie jest takie, że pierwszy kwadrat zrobiłem z kafelków 4x8 (i brakowało mi jednego), a drugi z kafelków 3x6 i zostało mi 13. Mam 31 kafelków.

Gotowane zagadki

W żargonie miłośników zagadek logiczno-matematycznych, kiedy ktoś odkryje lepsze lub inne rozwiązanie niż „oficjalne”, mówi się, że „ugotował” problem. Na przykład Fuster i Montesinos jeszcze bardziej urozmaicili podróżnym cierpiącym na klaustrofobię, wskazując, że oprócz wsiadania do ostatniego wagonu, mogą oni też biec naprzód, by zminimalizować czas spędzony w tunelu. A Luis Miguel Barros zauważa, że ​​jego piętnastoletnia córka zauważyła, że ​​skoro w oświadczeniu nie sprecyzowano tego, kwadrat domina nie musi być wypełniony: może to być rama domina, co prowadzi do nowych i ciekawych rozwiązań. Ignacio Alonso zauważa, że ​​podróżni cierpiący na klaustrofobię mogą woleć jak najszybciej zapomnieć o nieprzyjemnych doświadczeniach, dlatego wybiorą pierwszy wagon.

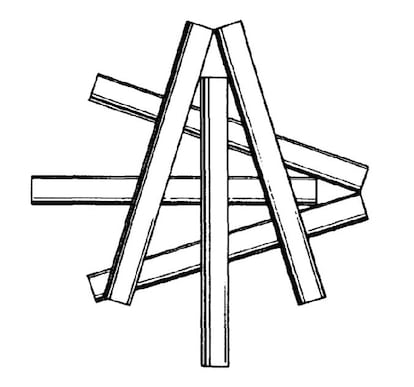
Jednym z najsłynniejszych problemów, o których mówiliśmy już parę lat temu, jest kontakt papierosów z żywnością. Przez pewien czas uważano, że maksymalnie 6 papierosów można ułożyć tak, aby każdy stykał się ze wszystkimi pozostałymi, jak pokazano na rysunku; ale potem pojawiło się rozwiązanie z numerem 7 (możesz je znaleźć?).

I od prostego gotowania przeszliśmy do wyrafinowanej kuchni matematycznej, ponieważ ktoś zadał pytanie, ile równych cylindrów można by zetknąć, gdyby ich końce nie mogły być wykorzystane, tzn. gdyby miały nieskończoną długość (ile według ciebie jest ich więcej?).

I po raz kolejny to, co wydawało się prostą matematyczną zabawą, okazało się mieć związek z materiałami auxetycznymi, czyli takimi, które mają ujemny współczynnik Poissona , co oznacza, że ​​w przeciwieństwie do gumki recepturki czy gumy do żucia, gdy są rozciągane, rozszerzają się, a nie zwężają. Ale to temat na inny artykuł...