Acht Lösungen

Die Nichttransitivität von Freundschaften (trotz des bekannten Sprichworts „Die Freunde meiner Freunde sind meine Freunde“), die vor einigen Wochen angesprochen wurde , hängt eindeutig mit dem Sorites-Paradoxon zusammen. Denn zwischen zwei Menschen besteht immer eine „Distanz“ (in Bezug auf Ideen, Charakter, Verhalten usw.), wie klein sie auch sein mag. Daher kann die Summe der Nähen zu einer unüberwindbaren Distanz werden, genauso wie ein Geschäft, das in der Nähe eines Geschäfts liegt, das in der Nähe eines Geschäfts liegt, das in der Nähe eines Geschäfts liegt, das in der Nähe Ihres Hauses liegt, am anderen Ende der Stadt liegen kann, wenn wir genügend Nähen dazwischenstellen.

Zu den acht Themen der letzten Woche einige schnelle oder nur skizzenhafte Antworten und andere ausführlichere:

1. Uns wird gesagt, dass die Frau keine dunkle Haut hat, und die Person mit den blonden Haaren antwortet, also muss sie weiße Haare haben, ergo …

2. Was die Teilung des stumpfen Dreiecks in spitze Winkel betrifft, gelangt man leicht zu dem falschen Schluss, dass dies unmöglich sei (Martin Gardner sagte, er habe zu seiner Zeit mehrere „Demonstrationen“ dieser Unmöglichkeit erhalten), denn egal, wie oft wir es teilen, am Ende bleibt immer mindestens ein kleiner und hartnäckiger stumpfer Winkel übrig, wie der am unteren rechten Scheitelpunkt der Abbildung.

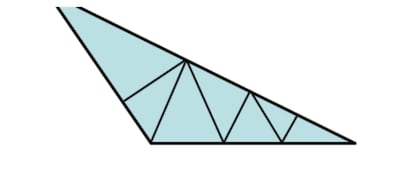
Eine Teilung ist jedoch möglich. Als Anhaltspunkt möchte ich sagen, dass es sich um eines jener lehrreichen Probleme handelt, bei denen wir uns unbewusst mehr Bedingungen auferlegen, als wir erfüllen sollen. Was ist in diesem Fall die unbewusste, nicht geforderte Bedingung?

3. Es gab fünf Marx Brothers: Chico, Groucho, Harpo, Gummo und Zeppo. Für unser Rätsel ist die wahrscheinlichste Lösung, dass es vier waren (wie in ihren bekanntesten Filmen) und drei von ihnen Linkshänder waren. Diese Lösung ist nicht eindeutig: Es könnten auch 21 Brüder gewesen sein, von denen 15 Linkshänder waren. Gibt es eine andere Lösung, auch wenn sie demografisch unwahrscheinlich ist?

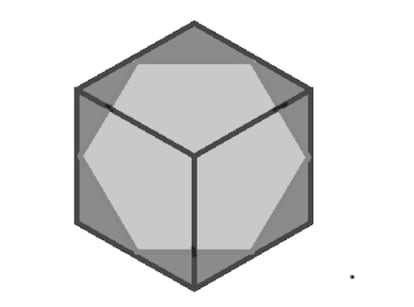
4. Wenn die Schnittebene durch die Mittelpunkte von sechs Kanten des Würfels verläuft, erhalten wir ein regelmäßiges Sechseck.

5. 129 + 438 = 567 (Ist diese Lösung eindeutig?).

6. Wenn OODDF die Quadratwurzel von WONDERFUL ist, kann O nicht größer als 2 sein, da sein Quadrat zehn Ziffern hätte, und es kann nicht 1 sein, da das Quadrat einer Zahl, die mit 11 beginnt, keine 1 in der zweiten Ziffer haben kann; daher ist O = 2. Die gesuchte Zahl liegt daher zwischen den Quadraten von 22.000 und 23.000, und da die zweite Ziffer von WONDERFUL 2 ist, ist W = 5… Wenn wir dieser Argumentation folgen, erhalten wir WONDERFUL = 523.814.769.

7. Der größte Kreis, der nur durch weiße Quadrate verläuft, hat seinen Mittelpunkt im Mittelpunkt eines weißen Quadrats und verläuft durch die am weitesten voneinander entfernten Eckpunkte der vier ihn umgebenden schwarzen Quadrate. (Wie groß ist sein Radius?)

8. Die Züge nähern sich mit einer Relativgeschwindigkeit von 130 + 170 = 300 km/h. Fünf Minuten vor der Kollision sind sie also 25 km voneinander entfernt. Der anfängliche Abstand ist irrelevant; er dient lediglich der Irreführung.

Nicht-transitive Spiele

Salva Fuster kommentierte die Nichttransitivität folgendermaßen: „Nichttransitive Würfel sind einer der überraschendsten Fälle, die ich kenne. Ich glaube, die meisten Leute, die zum ersten Mal nichttransitive Würfel sehen, versuchen den Fehler zu finden, indem sie die Fälle zählen, in denen ein Würfel einen anderen schlägt.“ Sehr zutreffend und interessant, so sehr, dass sich ein zukünftiger Beitrag diesem Thema widmen sollte. Und um Ihren Appetit anzuregen, denken Sie an ein anderes nichttransitives Spiel. Es gibt mindestens zwei sehr beliebte …